Lors d’un précédent article, nous avons expliqué pourquoi le calcul en capacité (ou calcul à la rupture) se répandait de plus en plus pour l’analyse des Etats Limites Ultimes (ELU). Les résultats fournis par ce type d’analyse n’étant pas habituels, cet article détaille comment les interpréter.
1) Rappels sur le calcul en capacité
Le principe du calcul en capacité est de trouver l’état à la ruine d’une structure en « court-circuitant » les phases élastique et élasto-plastique. Aucune information sur l’élasticité du matériau n’est donc nécessaire, on accepte une ductilité parfaite, et on limite la valeur des contraintes en fonction d’un critère : une traction/compression maximale ou un moment plastique limite pour un élément de poutre, une contrainte équivalente de Von Mises pour un cas 3D en acier, des contraintes principales bornées pour du béton, etc… C’est pour cette raison que l’on parle aussi de calcul rigide-plastique.
Ainsi, les résultats doivent toujours être analysés en gardant en tête ces hypothèses : on visualise un mécanisme purement plastique (le mécanisme de ruine) et une distribution de contraintes (ou forces) en équilibre avec la charge ultime.
De plus, la valeur du chargement extérieur importe peu, seule la « direction » du chargement importe : effort normal seul, couplage effort normal/moment de flexion, combinaison ELU avec concomitances, etc… Le calcul à la rupture nous permet d’encadrer le coefficient maximal à mettre sur ce chargement pour évaluer l’état limite (i.e. pour un chargement deux fois plus important, on trouve un coefficient deux fois plus petit).
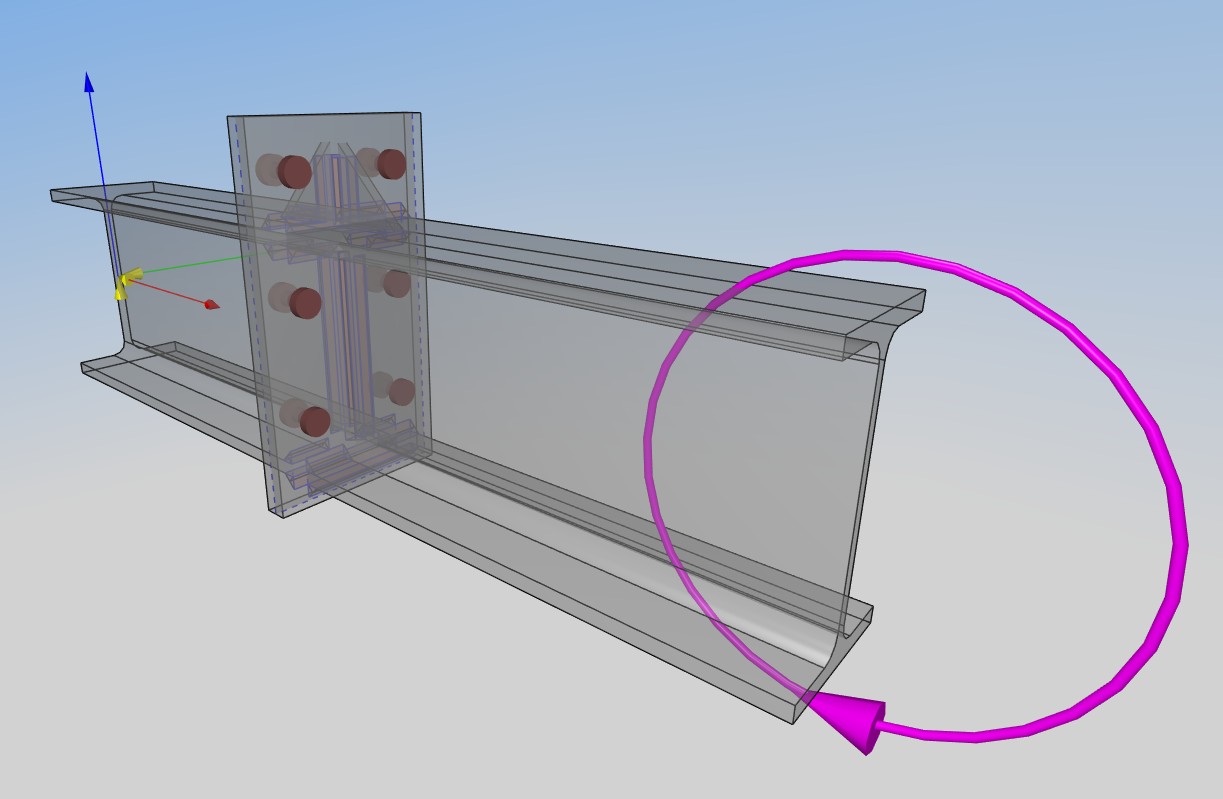
Étudions plus en détails un résultat de calcul à la rupture sur l’assemblage métallique suivant modélisé par DS STEEL. On applique un moment pur de 1MNm à une extrémité, l’autre étant encastrée.
2) Mécanisme de ruine
Sans entrer dans les détails théoriques, le mécanisme trouvé est celui qui minimise l’énergie de déformation plastique. Ainsi, le calcul à la rupture nous informera comment une structure va casser et s’écouler plastiquement.
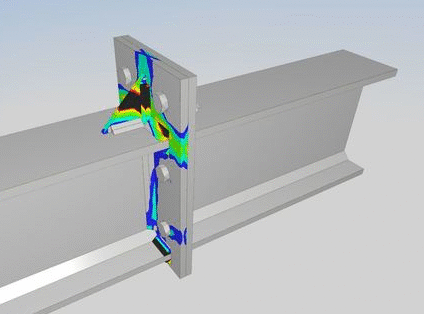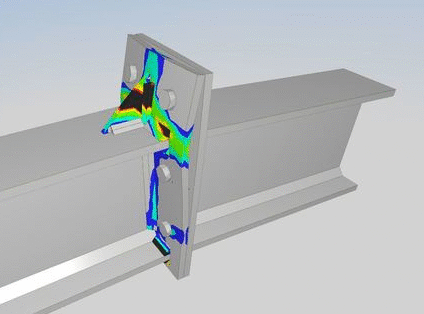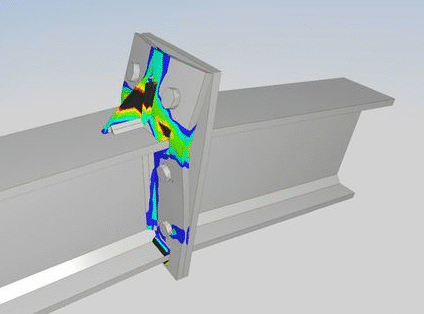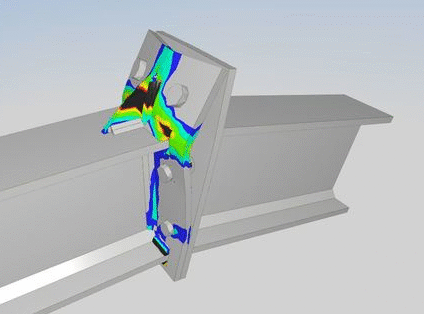
Par exemple ici, la ruine correspondant à l’apparition de plusieurs charnières plastiques sur une platine et à l’arrachement des boulons.

On comprend ainsi de manière très visuelle où se situent les zones les plus faibles de l’assemblage. Un calcul élastique sur ce même assemblage permet de voir l’ensemble de la connexion se déformer mais ne fait pas ressortir nettement les vulnérabilités.

Enfin, l’énergie trouvée dans ce calcul correspond à la borne supérieure du coefficient de charge maximal. On trouve ici 8.53e-3, soit 8.53kNm puisque le couple appliqué est de 1MNm. On peut donc affirmer que le moment limite supportable est inférieur à 8.53kNm.
Remarque : Il est à noter que le mécanisme trouvé aurait pu se situer sur l’autre platine, l’énergie de rupture plastique étant par symétrie la même.
3) Etat de contraintes
L’état de contrainte trouvé est en équilibre avec la charge maximale possible tout en respectant les limites du matériau. Dans l’exemple actuel, on respecte le critère tridimensionnel de Von Mises ainsi que des conditions de contact entres certaines surfaces. On observe des distributions de contraintes de flexion d’axes vertical et horizontal dans la platine, et de la traction dans les boulons.
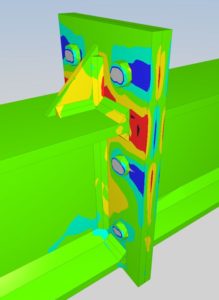


L’analyse fourni également une nouvelle valeur, borne inférieure du coefficient de charge maximal. On trouve ici 6.93e-3, soit 6.93kNm puisque le couple appliqué est toujours de 1MNm. On peut donc affirmer ici que le moment limite supportable est supérieur à 6.93kNm.
Un post-traitement de cet état d’équilibre permet d’effectuer les vérifications règlementaires, ce point sera abordé dans un autre article.
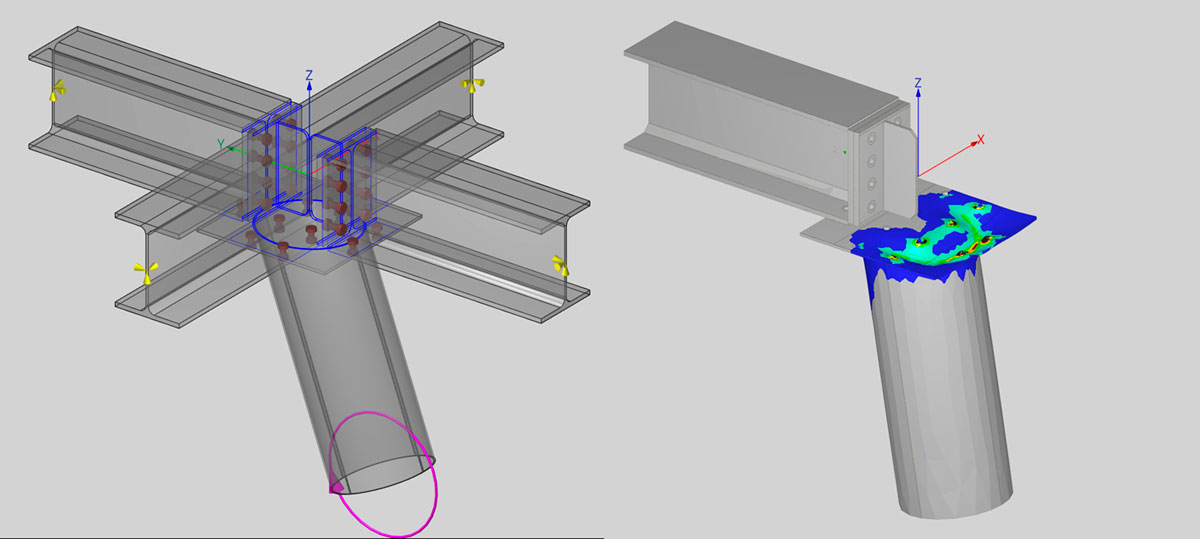
4) Poinçonnement d’une connexion tubulaire
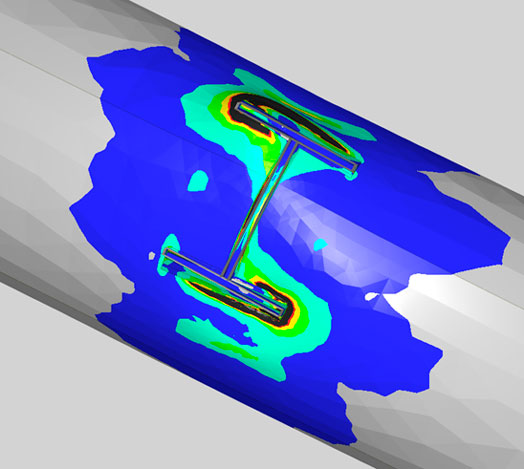
L’intérêt d’une approche numérique générale en capacité est que l’on peut obtenir des mécanismes de ruine pour n’importe quel assemblage et n’importe quel cas de charge. En particulier, l’exemple ci-dessous n’est pas conventionnel : il s’agit d’un montant en I soumis à un moment composé dévié connecté à un profilé tubulaire.
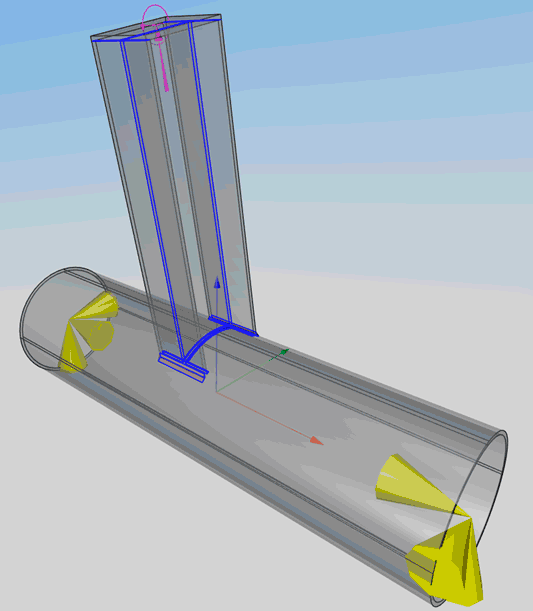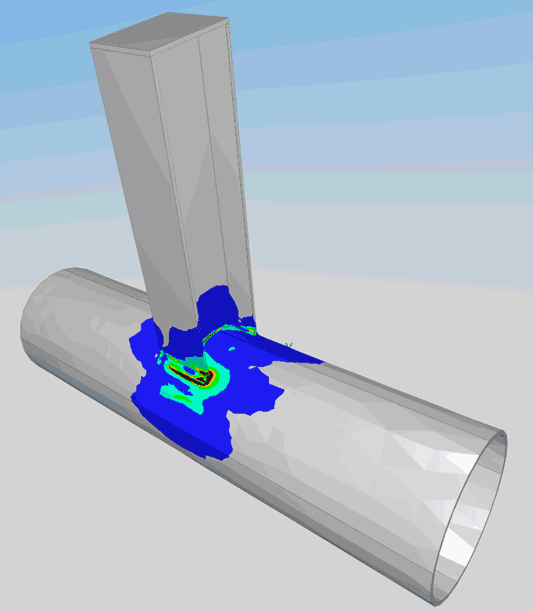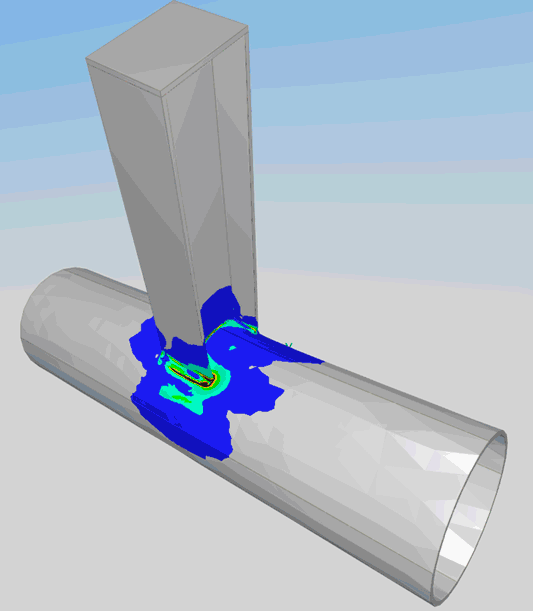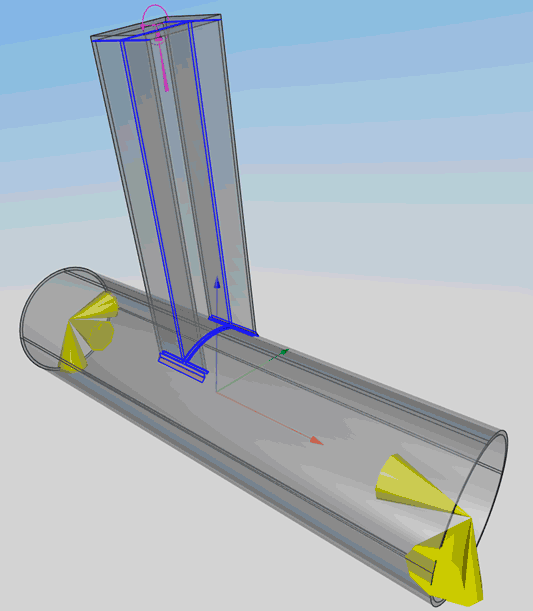
La lecture du mécanisme de ruine et des déformations plastiques permet de confronter son intuition, en particulier en ce qui concerne l’identification des lignes de rupture.
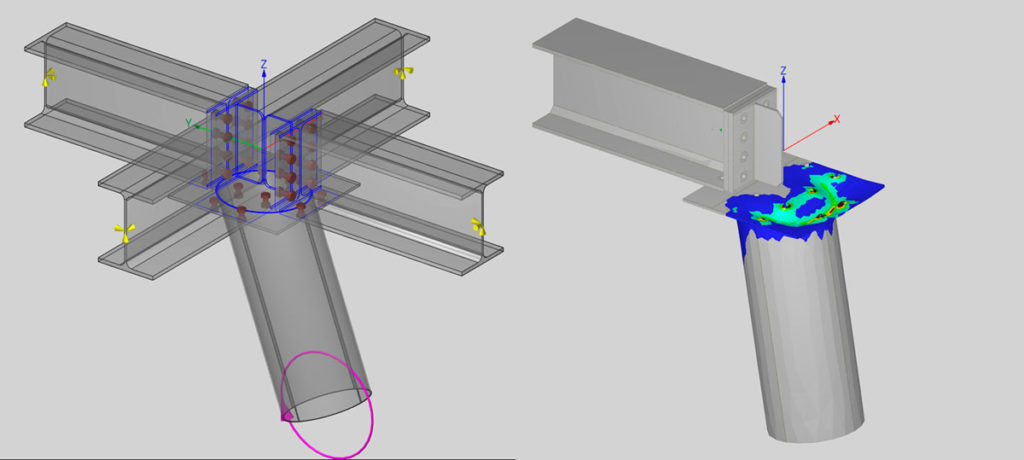
5) Exemple connexion tridimensionnelle
Un dernier exemple permet de mettre en évidence la différence de lecture des résultats entre un calcul élastique et un calcul en capacité. Le cas considéré est une connexion tridimensionnelle où l’on applique un moment simple dans le tube.
La déformation élastique de l’assemblage montre un décollement important de la platine de liaison du tube au reste de la connexion, ainsi qu’un cisaillement des raidisseurs de la poutre principale. On observe également des décollements légers des autres connexions boulonnés et des cisaillements de ces boulons.
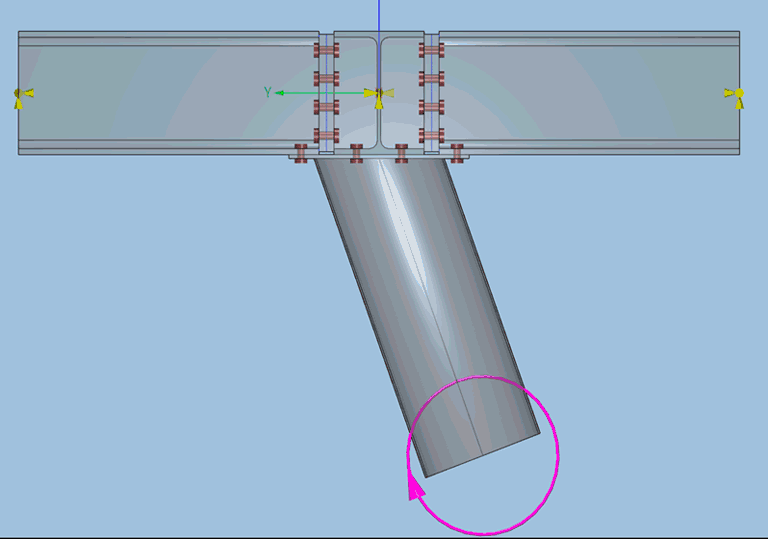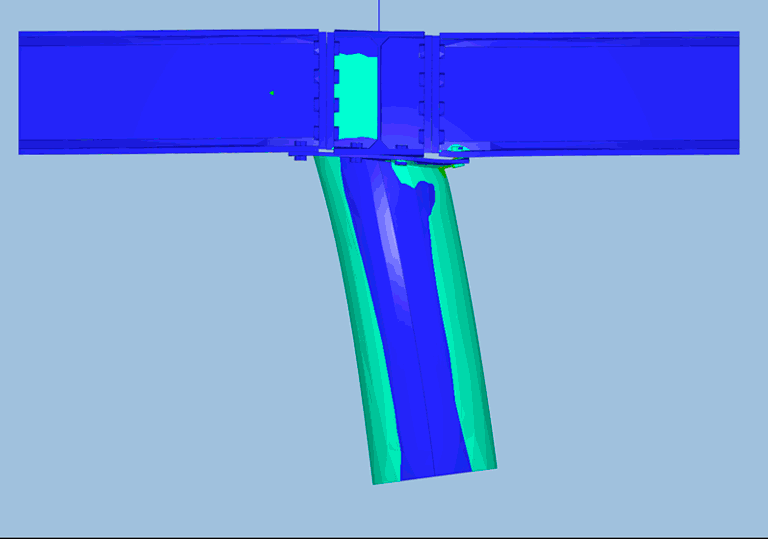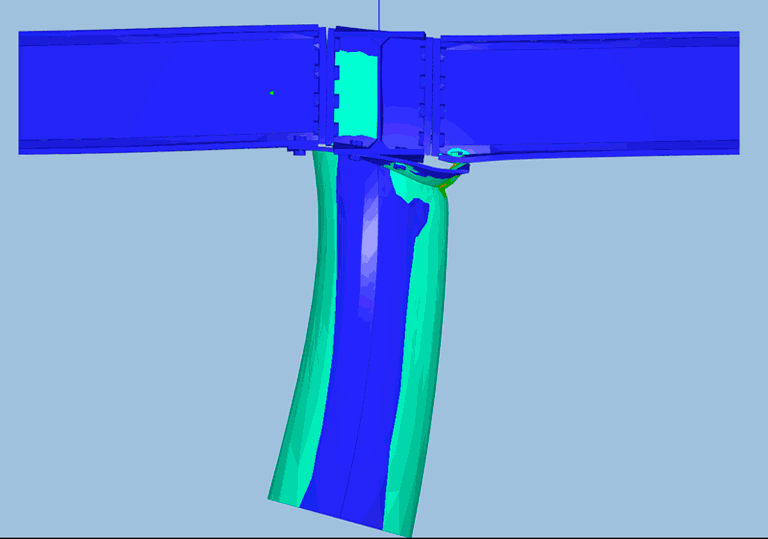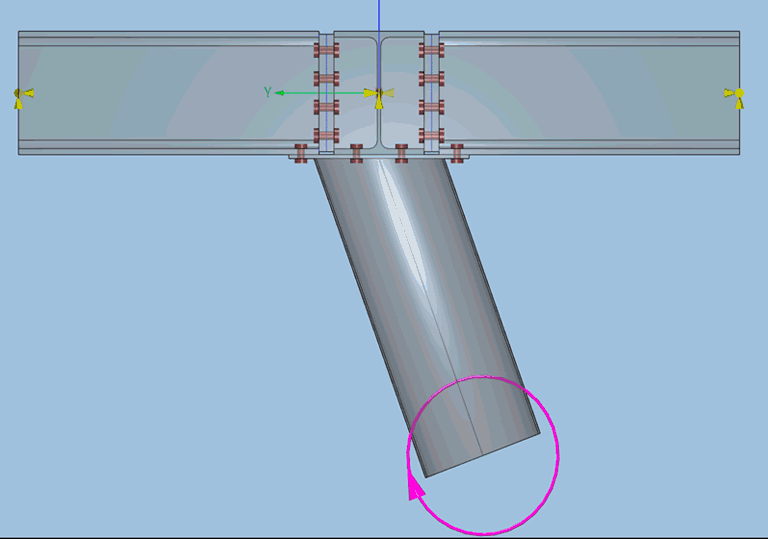
Au contraire, le mécanisme de ruine obtenu, ne met en évidence la déformation que d’une partie de la structure. Il s’agit de la partie de structure qui a atteint sa capacité plastique: la platine en flexion et le tube en compression. Tout le reste de la structure ne subit pas de plasticité (éléments représentés en gris) et donc est « immobile » dans le mécanisme de ruine.
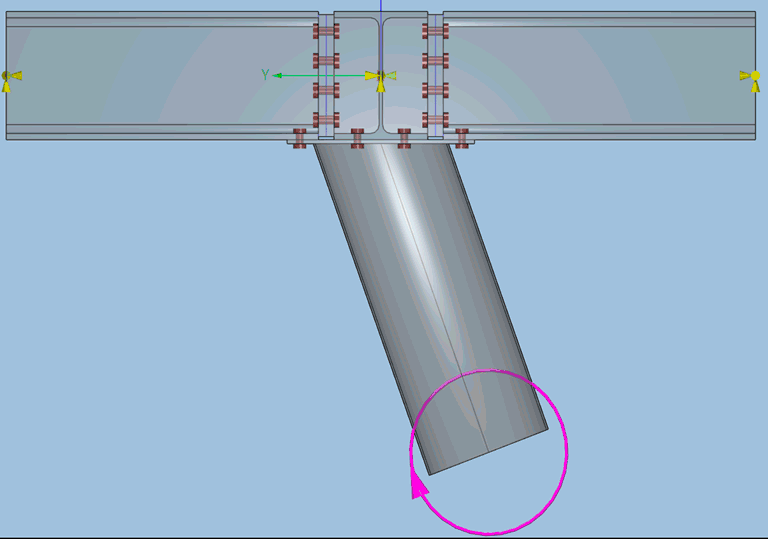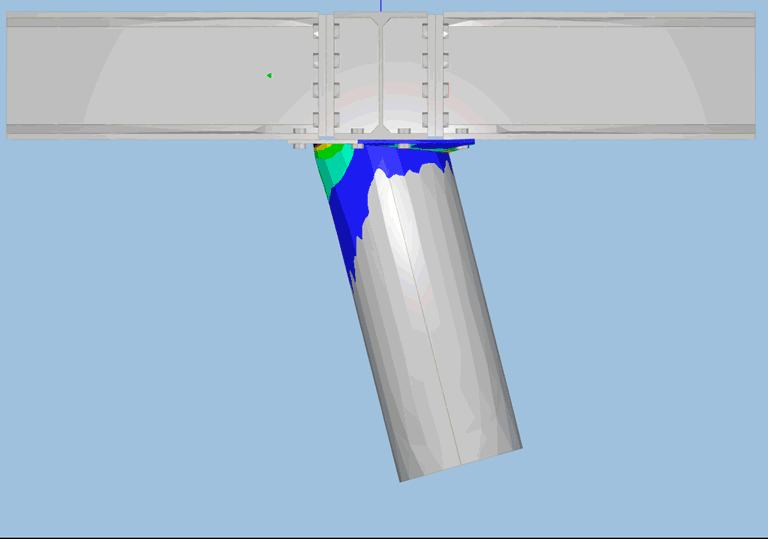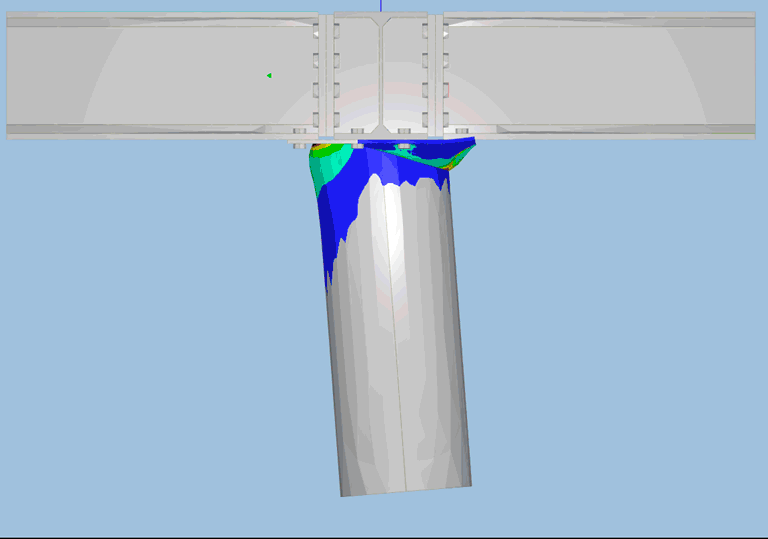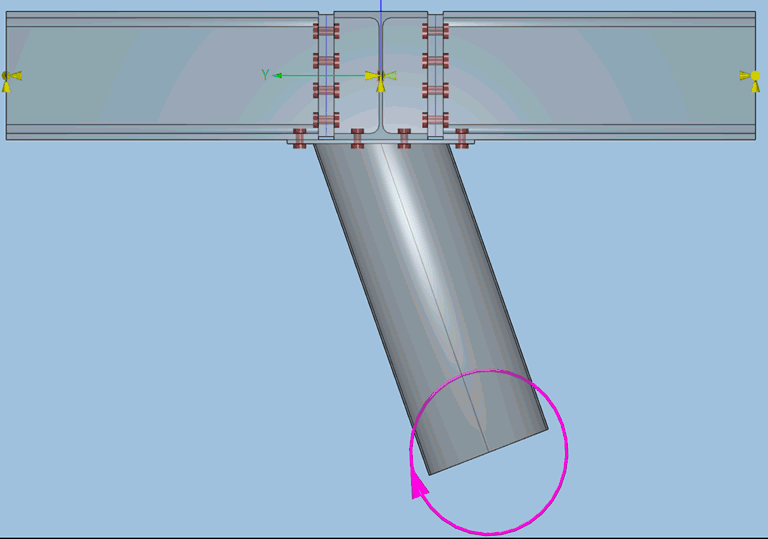
Une observation plus attentive de la zone plastifiée permet d’identifier les lignes de rupture: une ligne qui relie la rangée de boulon, et une partie d’arc qui passe par une autre rangée de boulon. Ce type de résultat est impossible à obtenir avec des calculs élastiques et très difficile à obtenir avec les calculs élasto-plastiques traditionnels.
L’analyse en capacité semble fournir moins d’information qu’une analyse élastique ou élasto-plastique, mais elle fourni l’information importante: les concentrations des zones plastiques et les vulnérabilités. De plus elle aide à voir le comportement de connexions non conventionnelles.
6) Conclusion
Le calcul en capacité nous informe de manière très concrète des faiblesses de la structure et d’un encadrement du moment limite. pour l’exemple de la connexion poutre-poutre, le moment résistant est compris entre 6.93kNm et 8.53kNm. Une analyse élastique n’aurait pas permis d’avoir les mêmes conclusions, les contraintes n’étant pas limitées. Une analyse classique élasto-plastique avec contacts aurait pu se rapprocher, difficilement, du palier plastique mais au prix d’heures passées à modéliser et régler la convergence numérique. De plus, les algorithmes traditionnellement utilisés ne précisent pas la confiance à avoir sur les résultats : selon les méthodes numériques employées, la charge limite peut-être au-dessus ou en-dessous de l’état trouvé.
Seule l’analyse en capacité fournit cette certitude sur l’état limite et une compréhension visuelle du comportement des structures.